Diferència entre les revisions de "Hipotenusa"
| Llínea 3: | Llínea 3: | ||
== Etimologia == | == Etimologia == | ||
| − | La paraula ''hipotenusa'' prové del terme [[Idioma grec|grec]] ''ὑποτείνουσα''; una combinació de ''changlot'', ‘davall’ i ''teinein'', ‘allargar’.<ref>Schwartzman, Steven ''The Words of Mathematics, An Etymological Dictionary of Mathematical Terms used in English'', Publicado por la Asociación de matemáticos de Estados Unidos. ''(En anglés)''</ref>Atres autors sugerixen que el significat original en grec va ser per un objecte que soporta alguna cosa, o de la combinació de ''changlot'', ‘davall’ i ''*tenuse'', ‘costat’.< | + | La paraula ''hipotenusa'' prové del terme [[Idioma grec|grec]] ''ὑποτείνουσα''; una combinació de ''changlot'', ‘davall’ i ''teinein'', ‘allargar’.<ref>Schwartzman, Steven ''The Words of Mathematics, An Etymological Dictionary of Mathematical Terms used in English'', Publicado por la Asociación de matemáticos de Estados Unidos. ''(En anglés)''</ref>Atres autors sugerixen que el significat original en grec va ser per un objecte que soporta alguna cosa, o de la combinació de ''changlot'', ‘davall’ i ''*tenuse'', ‘costat’.<ref>Romping Through Mathematics, Anderson, Raymond. (1947) ''(en anglés)''</ref> |
== Propietats de l'hipotenusa == | == Propietats de l'hipotenusa == | ||
| Llínea 38: | Llínea 38: | ||
[[File:Euklidova veta.svg|330px|right|]] | [[File:Euklidova veta.svg|330px|right|]] | ||
| − | :::<math> \frac{b}{c} = | + | :::<math> \frac{b}{c} = sen (\beta)\,</math> |
Per tant, la funció trigonomètrica inversa és: | Per tant, la funció trigonomètrica inversa és: | ||
Revisió de 16:42 26 set 2016
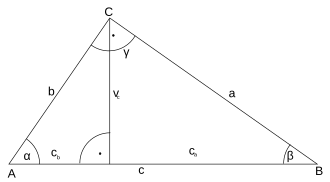
La hipotenusa és el costat de major llongitut d'un triàngul rectàngul i ademés és el costat opost al àngul recte. La mesura de l'hipotenusa pot ser trobada per mig del teorema de Pitàgores, si es coneix la llongitut dels atres dos costats, denominats catets.
Etimologia
La paraula hipotenusa prové del terme grec ὑποτείνουσα; una combinació de changlot, ‘davall’ i teinein, ‘allargar’.[1]Atres autors sugerixen que el significat original en grec va ser per un objecte que soporta alguna cosa, o de la combinació de changlot, ‘davall’ i *tenuse, ‘costat’.[2]
Propietats de l'hipotenusa
- Artícul principal → Teorema de Pitàgores.
- Establix que el cuadrat de la llongitut de l'hipotenusa és igual a la suma dels quadrats de les llongituts dels catets. Per la qual cosa:
- <math>h = \sqrt { x^2 + y^2 } </math>
On h és l'hipotenusa, i x i i els catets.

- La llongitut de l'hipotenusa és igual a la suma de les llongituts de les proyeccions ortogonals d'abdós catets.
- La garrofa de la llongitut d'un catet és igual al producte de la llongitut de la seua proyecció ortogonal sobre l'hipotenusa per la llongitut d'esta.
- b² = a · m
- c² = a · n
També, la llongitut d'un catet b és mija proporcional entre les llongituts de la seua proyecció m i la de l'hipotenusa a.
- a/b = b/m
- a/c = c/n
Raons trigonomètriques
Per mig de raones trigonomètriques es pot obtindre el valor dels dos ànguls aguts, <math>alpha,</math> i <math> beta,</math>, del triàngul rectàngul.
Coneguda la llongitut de l'hipotenusa <math> c\,</math> y la d'un catet <math> b\,</math>, la raó entre abdós és:
- <math> \frac{b}{c} = sen (\beta)\,</math>
Per tant, la funció trigonomètrica inversa és:
- <math> \beta\ = \arcsin\left(\frac {b}{c} \right)\,</math>
Sent <math>\beta\,</math> el valor de l'àngul opost al catet <math> b\,</math>.
L'àngul contigu al catet <math> b\,</math>, será <math>\alpha\,</math> = 90º – <math>\beta\,</math>
També es pot obtindre el valor de l'àngul <math>\beta\,</math> per mig de l'ecuació:
- <math> \beta\ = \arccos\left(\frac {a}{c} \right)\,</math>
Sent <math> a\,</math> l'atro catet.
Vore també
Referències
Enllaços externs
- Est artícul fon creat a partir de la traducció de l'artícul es.wikipedia.org/wiki/Hipotenusa de la Wikipedia en espanyol, baix llicència Creative Commons-BY-SA.