Diferència entre les revisions de "Hipotenusa"
(Pàgina nova, en el contingut: «right La '''hipotenusa''' és el costat de major llongitut d'un triàngul rectàngul i ademés és el costat opost al ...») |
|||
| (No es mostren 9 edicions intermiges d'3 usuaris) | |||
| Llínea 1: | Llínea 1: | ||
[[Image:Triangulo-Rectangulo.png|right]] | [[Image:Triangulo-Rectangulo.png|right]] | ||
| − | + | L''''hipotenusa''' és el costat de major llongitut d'un [[triàngul rectàngul]] i ademés és el costat opost a l'[[àngul recte]]. La mesura de l'hipotenusa pot ser trobada per mig del [[teorema de Pitàgores]], si es coneix la llongitut dels atres dos costats, denominats [[catet]]s. | |
== Etimologia == | == Etimologia == | ||
| − | La paraula ''hipotenusa'' prové del terme [[Idioma grec|grec]] ''ὑποτείνουσα''; una combinació de ''changlot'', | + | La paraula ''hipotenusa'' prové del terme [[Idioma grec|grec]] ''ὑποτείνουσα''; una combinació de ''changlot'', ‘devall’ i ''teinein'', ‘allargar’.<ref>Schwartzman, Steven ''The Words of Mathematics, An Etymological Dictionary of Mathematical Terms used in English'', Publicado por la Asociación de matemáticos de Estados Unidos. ''(En anglés)''</ref> Atres autors sugerixen que el significat original en grec va ser per un objecte que soporta alguna cosa, o de la combinació de ''changlot'', ‘devall’ i ''*tenuse'', ‘costat’.<ref>Romping Through Mathematics, Anderson, Raymond. ([[1947]]) ''(en anglés)''</ref> |
== Propietats de l'hipotenusa == | == Propietats de l'hipotenusa == | ||
{{AP|Teorema de Pitàgores}} | {{AP|Teorema de Pitàgores}} | ||
| − | * Establix que el | + | * Establix que el quadrat de la llongitut de l'hipotenusa és igual a la suma dels quadrats de les llongituts dels catets. Per lo que: |
:<math>h = \sqrt { x^2 + y^2 } </math> | :<math>h = \sqrt { x^2 + y^2 } </math> | ||
| − | + | A on '''''h''''' és l'hipotenusa, i '''''x''''' i '''''i''''' els catets. | |
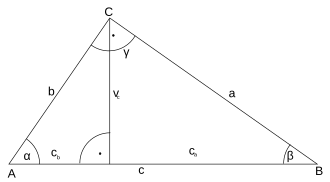
[[Image:Triângulo retângulo.svg|225px|thumb|right|En la figura, l'hipotenusa és el costat '''a''' i els [[catet]]s són els costats '''b''' i '''c'''. La proyecció ortogonal de '''b''' és '''m''', i la de '''c''' és '''n'''.]] | [[Image:Triângulo retângulo.svg|225px|thumb|right|En la figura, l'hipotenusa és el costat '''a''' i els [[catet]]s són els costats '''b''' i '''c'''. La proyecció ortogonal de '''b''' és '''m''', i la de '''c''' és '''n'''.]] | ||
| Llínea 20: | Llínea 20: | ||
* La llongitut de l'hipotenusa és igual a la suma de les llongituts de les proyeccions ortogonals d'abdós catets. | * La llongitut de l'hipotenusa és igual a la suma de les llongituts de les proyeccions ortogonals d'abdós catets. | ||
| − | * La | + | * La llongitut d'un catet és igual al producte de la llongitut de la seua proyecció ortogonal sobre l'hipotenusa per la llongitut d'esta. |
| Llínea 38: | Llínea 38: | ||
[[File:Euklidova veta.svg|330px|right|]] | [[File:Euklidova veta.svg|330px|right|]] | ||
| − | :::<math> \frac{b}{c} = | + | :::<math> \frac{b}{c} = sen (\beta)\,</math> |
Per tant, la funció trigonomètrica inversa és: | Per tant, la funció trigonomètrica inversa és: | ||
| Llínea 58: | Llínea 58: | ||
* [[Catet]] | * [[Catet]] | ||
* [[Círcul unitari]] | * [[Círcul unitari]] | ||
| − | + | ||
== Referències == | == Referències == | ||
| − | {{ | + | {{Reflist}} |
== Enllaços externs == | == Enllaços externs == | ||
{{Wikcionario}} | {{Wikcionario}} | ||
| + | [[Categoria:Geometria]] | ||
[[Categoria:Geometria del triàngul]] | [[Categoria:Geometria del triàngul]] | ||
{{Traduït de|es|Hipotenusa}} | {{Traduït de|es|Hipotenusa}} | ||
Última revisió del 11:27 9 jul 2024
L'hipotenusa és el costat de major llongitut d'un triàngul rectàngul i ademés és el costat opost a l'àngul recte. La mesura de l'hipotenusa pot ser trobada per mig del teorema de Pitàgores, si es coneix la llongitut dels atres dos costats, denominats catets.
Etimologia[editar | editar còdic]
La paraula hipotenusa prové del terme grec ὑποτείνουσα; una combinació de changlot, ‘devall’ i teinein, ‘allargar’.[1] Atres autors sugerixen que el significat original en grec va ser per un objecte que soporta alguna cosa, o de la combinació de changlot, ‘devall’ i *tenuse, ‘costat’.[2]
Propietats de l'hipotenusa[editar | editar còdic]
- Artícul principal → Teorema de Pitàgores.
- Establix que el quadrat de la llongitut de l'hipotenusa és igual a la suma dels quadrats de les llongituts dels catets. Per lo que:
- <math>h = \sqrt { x^2 + y^2 } </math>
A on h és l'hipotenusa, i x i i els catets.

- La llongitut de l'hipotenusa és igual a la suma de les llongituts de les proyeccions ortogonals d'abdós catets.
- La llongitut d'un catet és igual al producte de la llongitut de la seua proyecció ortogonal sobre l'hipotenusa per la llongitut d'esta.
- b² = a · m
- c² = a · n
També, la llongitut d'un catet b és mija proporcional entre les llongituts de la seua proyecció m i la de l'hipotenusa a.
- a/b = b/m
- a/c = c/n
Raons trigonomètriques[editar | editar còdic]
Per mig de raones trigonomètriques es pot obtindre el valor dels dos ànguls aguts, <math>alpha,</math> i <math> beta,</math>, del triàngul rectàngul.
Coneguda la llongitut de l'hipotenusa <math> c\,</math> y la d'un catet <math> b\,</math>, la raó entre abdós és:
- <math> \frac{b}{c} = sen (\beta)\,</math>
Per tant, la funció trigonomètrica inversa és:
- <math> \beta\ = \arcsin\left(\frac {b}{c} \right)\,</math>
Sent <math>\beta\,</math> el valor de l'àngul opost al catet <math> b\,</math>.
L'àngul contigu al catet <math> b\,</math>, será <math>\alpha\,</math> = 90º – <math>\beta\,</math>
També es pot obtindre el valor de l'àngul <math>\beta\,</math> per mig de l'ecuació:
- <math> \beta\ = \arccos\left(\frac {a}{c} \right)\,</math>
Sent <math> a\,</math> l'atro catet.
Vore també[editar | editar còdic]
Referències[editar | editar còdic]
Enllaços externs[editar | editar còdic]
- Est artícul fon creat a partir de la traducció de l'artícul es.wikipedia.org/wiki/Hipotenusa de la Wikipedia en espanyol, baix llicència Creative Commons-BY-SA.