Diferència entre les revisions de "Teorema dels sens"
| Llínea 13: | Llínea 13: | ||
{{Equació|<math>(sen,A)=sen,P=\frac{BC}{BP} = \frac{a}{2R}</math>|3=left}} | {{Equació|<math>(sen,A)=sen,P=\frac{BC}{BP} = \frac{a}{2R}</math>|3=left}} | ||
on ''R'' és el radi de la [[circumferència]]. Rebujant ''2R'' obtenim: | on ''R'' és el radi de la [[circumferència]]. Rebujant ''2R'' obtenim: | ||
| − | {{Equació|<math>\frac{a}{ | + | {{Equació|<math>\frac{a}{sen\,A} = 2R</math>|3=left}}. |
== Vore també == | == Vore també == | ||
Revisió de 13:49 29 ago 2016
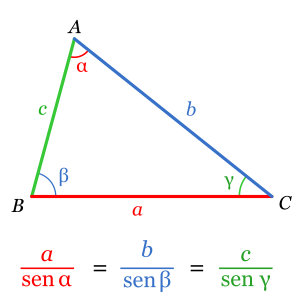
En trigonometria, la teorema dels sens[1] o també conegut com a llei dels sens [2] és una relació de proporcionalitat entre les llongituts dels costats d'un triàngul i els sens dels seus respectius ànguls oposts. Usualment es presenta de la següent forma: Plantilla:T.
Demostració
A pesar de ser dels teoremas trigonomètrics més usats i de tindre una demostració particularment simple, és poc comú que es present o discutixca la mateixa en cursos de trigonometria, de modo que és poc coneguda.
Donat el triàngul ABC, denotem per O el seu circumcentre i dibuixem el seu circumferència circumscrita. Prolongant el segment BO fins a tallar la circumferència, s'obté un diàmetro BP.
Ara, el triàngul PCB és recte, ya que BP és un diàmetro, i ademés els ànguls A i P són congruents, perque abdós són ànguls inscrits que òbrin el segment BC (Vore definició de arc capaç). Per definició de la funció trigonomètrica sen, es té
{{{1}}}
on R és el radi de la circumferència. Rebujant 2R obtenim:
{{{1}}}
.
Vore també
- Est artícul fon creat a partir de la traducció de l'artícul es.wikipedia.org/wiki/Teorema de los senos de la Wikipedia en espanyol, baix llicència Creative Commons-BY-SA.